用人话讲明白支持向量机SVM的数学原理
1. 什么是SVM
SVM支持向量机,号称机器学习的拦路虎。江湖传言,遇到了他,机器学习就会从入门到放弃。另一方面也就是说,只要搞定了SVM,后面的算法模型学起来都是小意思。
先看下官方定义:
支持向量机方法是建立在统计学习理论的VC维理论和结构风险最小原理基础上的,根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折衷,以期获得最好的泛化能力。
VC 维,结构风险,有限样本,模型复杂性,最佳折衷,泛化能力,这一切……真是让人摸不着头脑……
行了,文绉绉的理论从来看不懂,我们还是从算法看起吧。
SVM一般用于解决二分类问题(也可以解决多分类和回归问题,本文暂不涉及),数学化语言概述如下:
样本数据:$n$个样本,$p$个输入 $(x_{1},\cdots,x_{p})$ ,1个输出$y$
第$i$个样本的输入: $X_{i}=(x_{i1},x_{i2},\cdots,x_{ip})^{T}, i=1,2,\cdots n$
输出$y$:一般用$1$和$-1$作为两类样本的标签
训练样本集$D$: \(D=\begin{pmatrix} x_{11}, & x_{12} , & x_{13} , & \cdots , & x_{1p}, & y_{1} \\x_{21} ,& x_{22} , & x_{23} , & \cdots , & x_{2p}, & y_{2} \\& & \cdots \\& & \cdots \\x_{n1} ,& x_{n2}, & x_{n3} , & \cdots , & x_{np}, & y_{n} \end{pmatrix}\)
训练目的:以训练样本为研究对象,在样本的特征空间中找到一个超平面 $W^{T}X+b=0$ ,将两类样本($+1$和$-1$)有效分开,其中 $W=(w_{1},w_{2},\cdots,w_{p})^{T}$
然而,这些个公式更是看的云里雾里。没关系,抽象的数学语言难以理解,那我们就从直观的图形和例子开始,抽丝剥茧一点点学。
2. 线性分类器的含义
上一篇学线性回归时,是从一元线性回归讲起。一元,即一个自变量,再加上一个因变量,这种数据形式在二维坐标轴中就可以表示成$(x,y)$。$(x,y)$的数据形式可以通过画点、画线在二维平面上进行展示,方便初学者理解。
学习算法时通过图的形式来入门,最合适不过。那么,我们讲SVM也从平面上的点和线讲起不就好了。
我们用图看看线性分类器要解决什么样的问题。
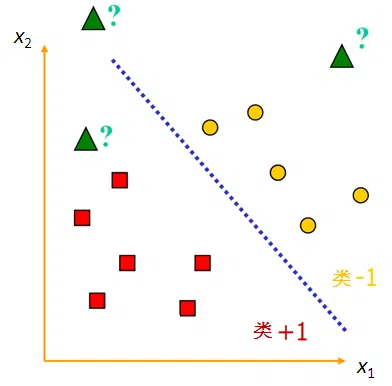
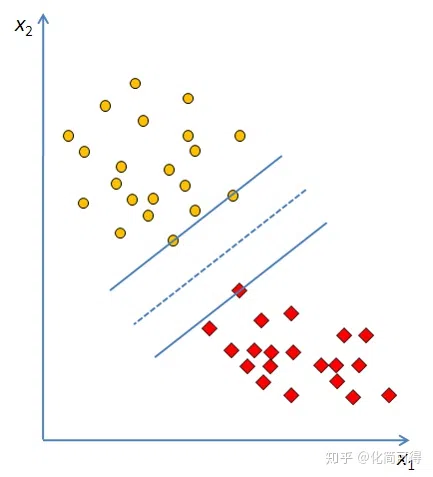
假设有两类要区分的样本点,一类用黄色圆点代表,另一类用红色方形代表,中间这条直线就是一条能将两类样本完全分开的分类函数。
用前面的数学化语言描述一下这个图,就是:
样本数据:11个样本,2个输入 $(x_{1},x_{2})$,一个输出$y$
第$i$个样本的输入: $X_{i}=(x_{i1},x_{i2})^{T}, i=1,2,\cdots 11$
输出$y$:用$+1$(红色方形)和$-1$(黄色圆点)作为标签
训练样本集$D$:
\[D=\begin{pmatrix} x_{11}, & x_{12} , & y_{1} \\x_{21} ,& x_{22} , & y_{2} \\&\cdots \\x_{n1} ,& x_{n2}, & y_{n} \end{pmatrix},n=11\]训练目的:以训练样本为研究对象,找到一条直线 $w_{1}x_{1}+w_{2}x_{2}+b=0$,将两类样本有效分开。
这里我们引出线性可分的定义:如果一个线性函数能够将样本分开,就称这些样本是线性可分的。线性函数在一维空间里,就是一个小小的点;在二维可视化图像中,是一条直直的线;在三维空间中,是一个平平的面;在更高维的空间中,是无法直观用图形展示的超平面。
回想一下线性回归,在一元线性回归中我们要找拟合一条直线,使得样本点$(x, y)$都落在直线附近;在二元线性回归中,要拟合一个平面,使得样本点$(x_1, x_2, y)$都落在该平面附近;在更高维的情况下,就是拟合超平面。
那么,线性分类(此处仅指二分类)呢?当样本点为$(x, y)$时(注意,和回归不同,由于$y$是分类标签,$y$的数字表示是只有属性含义,是没有真正的数值意义的,因此当只有一个自变量时,不是二维问题而是一维问题),要找到一个点$wx+b=0$,即$x=-b/w$这个点,使得该点左边的是一类,右边的是另一类。
当样本点为$(x_1, x_2, y)$时,要找到一条直线 $w_{1}x_{1}+w_{2}x_{2}+b=0$ ,将平面划分成两块,使得 $w_{1}x_{1}+w_{2}x_{2}+b>0$的区域是$y=1$类的点,$w_{1}x_{1}+w_{2}x_{2}+b<0$ 的区域是$y=-1$类别的点。
更高维度以此类推,由于更高维度的的超平面要写成$w_{1}x_{1}+w_{2}x_{2}+\cdots +w_{p}x_{p}+b=0$ 会有点麻烦,一般会用矩阵表达式代替,即上面的 $W^{T}X+b=0$ 。
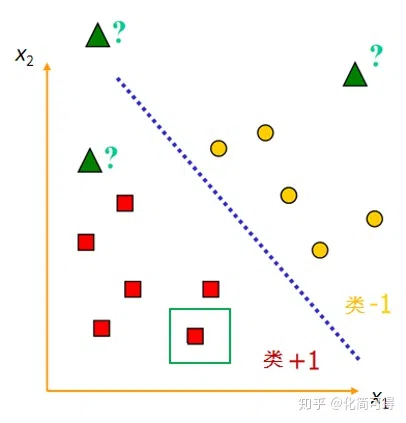
$W^{T}X+b=0$ 这个式子中,$X$不是二维坐标系中的横轴,而是样本的向量表示。例如上面举的二维平面中的例子,假设绿色框内是的坐标是$(3,1)$,则 $X^{T}=(x_{1},x_{2})=(3,1)$ 。一般说向量都默认是列向量,因此以行向量形式来表示时,就加上转置。因此, $W^{T}X+b=0$中$W^{T}$是一组行向量,是未知参数,$X$是一组列向量,是已知的样本数据,可以将 $w_{i}$理解为$x_{i}$的系数,行向量与列向量相乘得到一个$1\times 1$的矩阵,也就是一个实数。
3. 怎么找线性分类器
我们还是先看只有两个自变量的情况下,怎么求解最佳的线性分割。
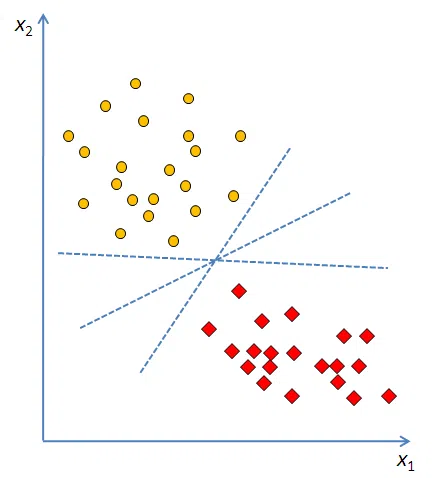
如图,理想状态下,平面中的两类点是完全线性可分的。这时问题来了,这样能把两类点分割的线有很多啊,哪条是最好的呢?
支持向量机中,对最好分类器的定义是:最大边界超平面,即距两个类别的边界观测点最远的超平面。在二维情况下,就是找最宽的马路,在三维问题中,就是找最厚的木板。
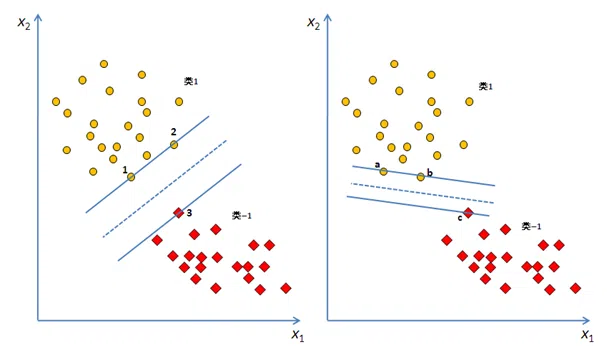
显然,上图中左边的马路比右边的宽,马路的边界由1、2、3这三个点确定,而马路中间那条虚线,就是我们要的 $W^{T}X+b=0$ 。
可以看到,我们找马路时,只会考虑$+1$类中,离$-1$类近的点,还有$-1$类中,离$+1$类距离近的点,即图中的1、2、3和$a$、$b$、$c$这些点。其他距离对方远的样本点,我们做支持向量机这个模型时,是不考虑的。
由于最大边界超平面仅取决于两类别的边界点,这些点被称为支持向量,因此这种算法被命名为支持向量机。这个定义就比较好理解了吧?
4. 求解超平面
上篇仅介绍了SVM的基本概念,本篇着重讲解SVM中的最佳线性分类器(最大边界超平面)是如何求得的。
4.1 几何间隔
上一小节给出二维问题下最佳线性分割的标准,就是分割线到两类边界点的距离最“宽”,那么这个“宽度”怎么量化和求解呢?
我们知道,点 $(x_{0} ,y_{0})$ 直线$Ax+By+c=0$的距离(中学的知识点),可以表示为:
\[D=\dfrac{|Ax_{0}+By_{0}+c|} {\sqrt{A^{2}+B^{2}}}\]在我们的二维问题中,第$i$个点的坐标为 $X_{i}=(x_{i1},x_{i2})^{T}$ ,直线为 $w_{1}x_{1}+w_{2}x_{2}+b=W^{T}X+b=0$ (为了打公式方便,后面不区分向量和其转置,省略$T$标志,统一写成 $WX+b=0$ ),将上式替换, $X_{i}$ 到分割直线的距离为:
\[D=\dfrac{|WX_{i}+b|} {\sqrt{w_{1}^{2}+w_{2}^{2}}}=\dfrac{|WX_{i}+b|}{\Vert W \Vert}\]有的人也许对分母$\Vert W\Vert $感到陌生,这里多做点解释。
$\Vert W \Vert $是向量$W$的“2-范数”( $L_{2}$ 范数),一般我们说向量长度,指的是向量的2-范数。例如这里的 $W=(w_{1},w_{2})$ ,它的2-范数就是 $\Vert W\Vert _{2}=\sqrt{w_1^2+w_2^2} $(通常会省略下标2,一般说$ \Vert W\Vert $就是指 $ \Vert W \Vert_2 $ ,而它的$p$-范数( $L_p$ 范数)就是 $\Vert W_p \Vert =\sqrt[p]{w_1^p+w_2^p}$ 。
这里给出向量范数的一般形式。对于$n$维向量 $W=(w_{1},w_{2},\cdots ,w_{n})$ ,它的$p$-范数为: \(\Vert W\Vert _{p}=\sqrt[p]{w_{1}^{p}+w_{2}^{p}+...+w_{n}^{p}}\)
$D=\dfrac{\vert WX_i+b\vert}{\Vert W \Vert}$这个公式的学名叫做几何间隔,几何间隔表示的是点到超平面的欧氏距离(还记得上次讲线性回归时强调要记住这个名称吧?)。
以上是单个点到某个超平面的距离定义(在这个具体的二维例子中是一条直线,我们认为直线也是属于超平面的一种,后面统一写超平面的时候,不要觉得混乱哦)。上一节我们说要求最宽的“宽度”,最厚的“厚度”,其实就是求支持向量到超平面的几何间隔最大值。
回到二维问题,令“马路宽度”为$2d$,即最佳分割线到两类支持向量的距离均为$d$,最佳分割线参数的求解目标就是使$d$最大。

4.2 凸二次规划
假设$L_1$是其中一条过$+1$类支持向量且平行于$WX+b=0$的直线,$L_2$是过$-1$类支持向量且平行于$WX+b=0$的直线,这$L_1$和$L_2$就确定了这条马路的两边,$L$是马路中线。
由于确定了$L$的形式是 $WX+b=0$,又因为$L_1$、$L_2$距离$L$是相等的,我们定义$L_1$为$WX+b=1$,$L_2$为$WX+b=-1$。为什么这两条平行线的方程右边是$1$和$-1$其实也可以是$2$和$-2$,或者任意非零常数$C$和$-C$,规定$1$和$-1$只是为了方便。就像$2x+3y+1=0$和$4x+6y+2=0$是等价的,方程同乘一个常数后并不会改变。
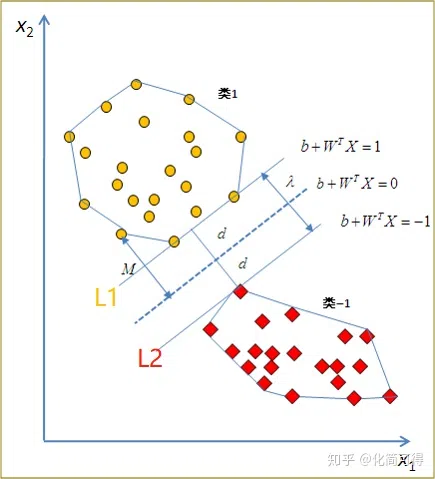
确定了三条线的方程,我们就可以求马路的宽度$2d$。$2d$是$L_1$和$L_2$这两条平行线之间的距离:
\[2d=\dfrac{\vert 1-(-1)\vert}{\Vert W\Vert }=\dfrac{2}{\Vert W\Vert }\]在4.1小节我们讲了现在的目标是最大化几何间隔$d$,由于 $d=\dfrac{1}{\Vert W\Vert}$ ,问题又转化成了最小化$\Vert W\Vert$。对于求$\min \Vert W\Vert$,通常会转化为求 $\min\dfrac{\Vert W\Vert^{2}}{2}$ ,为什么要用平方后除以2这个形式呢?这是为了后面求解方便(还记得上次讲线性回归讲到的凸函数求导吗?)。
$\Vert W\Vert$不可能无限小,因为还有限制条件呢。超平面正确分类意味着点$i$到超平面的距离恒大于等于$d$,即:
\[\frac{|WX_{i}+b|}{\Vert W\Vert}\geqslant d=\frac{1}{\Vert W\Vert}\]两边同乘$\Vert W\Vert$,简化为:
\[|WX_{i}+b|=y_{i}(WX_{i}+b) \geqslant 1\]$\vert WX_{i}+b \vert=y_{i}(WX_{i}+b)$ 应该不难理解吧?因为$y$只有两个值,$+1$和$-1$。
- 如果第$i$个样本属于$+1$类别, $y_{i}>0$,同时 $WX_{i}+b>0$ ,两者相乘也大于0;
- 若属于$-1$类, $y_{i}<0$,$WX_{i}+b<0$,此时相乘依旧是大于0的。
这意味着 $y_{i}(WX_{i}+b)$ 恒大于0,$y$起到的作用就和绝对值一样。之所以要用$y$替换绝对值,是因为$y$是已知样本数据,方便后面的公式求解。
我们将这个目标规划问题用数学语言描述出来。
目标函数: \(\min \tau(W) = \min \dfrac{1}{2} \Vert W\Vert ^2 = \min \dfrac{1}{2}W^TW\)
约束条件:
\[y_i(b+W^TX_i)-1 \geqslant 0, i=1,2,\cdots,n\]这里约束条件是$W$的多个线性函数($n$代表样本个数),目标函数是$W$的二次函数(再次提醒,$X$、$y$不是变量,是已知样本数据),这种规划问题叫做凸二次规划。
什么叫凸二次规划?之前讲线性回归最小二乘法时,提到了处处连续可导且有最小值的凸函数。从二维图形上理解“凸”,就是在一个“凸”形中,任取其中两个点连一条直线,这条线上的点仍然在这个图形内部,例如 $f(x)=x^{2}$ 上方的区域。
当一个约束优化问题中,目标函数和约束函数是凸函数(线性函数也是凸函数),该问题被称为凸优化问题。 当凸优化问题中的目标函数是一个二次函数时,就叫做凸二次规划,一般形式为: \(\begin{aligned} \min_x & \frac{1}{2}x^TQx + c^Tx \\ \text{ s.t. } & W_x \leqslant b \end{aligned}\)
若上式中的$Q$为正定矩阵,则目标函数有唯一的全局最小值。我们的问题中,$Q$是一个单位矩阵。
4.3 拉格朗日乘数法
这种不等式条件约束下的求多元函数极值的问题,到底怎么求解呢?
以下会涉及高等数学知识,推导过程较为复杂,数学基础较弱或对推导没兴趣的同学可以跳过,直接看第5小节
当我们求一个函数 $f(x,y)$ 的极值时,如果不带约束,分别对$x$,$y$求偏导,令两个偏导等于$0$,解方程即可。这种是求无条件极值。
带约束的话则为条件极值,如果约束为等式,有时借助换元法可以将有条件转化为无条件极值从而求解,不过换元消元也只能解决三元以内的问题。而拉格朗日乘数法可以通过引入新的未知标量(拉格朗日乘数 $\lambda$ ),直接求多元函数条件极值,不必先把问题转化为无条件极值的问题。
求函数$f(x,y)$在附加条件 $\varphi(x,y)=0$下可能的极值点,可以先做拉格朗日函数:
$L(x,y) = f(x,y) + \lambda \varphi (x,y)$,其中$\lambda$为参数,则各阶偏导为$0$: \(\begin{cases} f_x(x,y) + \lambda \varphi_x(x,y) = 0,\\ f_y(x,y) + \lambda \varphi_y(x,y) = 0,\\ \varphi(x,y) = 0 \end{cases}\) 则该方程组解出的$x, y, \lambda$就是函数$f(x,y)$在附件条件下的所有可能极值点。
讲完拉格朗日乘数法的思路,仍解决不了上面的问题,因为该问题约束条件是不等式。其实,解决办法很简单,分成两部分看就行。
为了看起来简洁,我们令目标函数 $\min\dfrac{\Vert W \Vert^{2}}{2}$为 $\min f(W)$,约束条件 $y_{i} (WX_{i}+b)-1\geqslant 0$为$g_{i}(W)\geqslant 0$ 。
- 当可行解$W$落在 $g_{i}(W)>0$ 区域内时,此时的问题就是求无条件极值问题(因为极小值已经包含在整个大区域内),直接极小化 $f(W)$就行;
- 当可行解$W$落在 $g_{i}(W)=0$区域内时,此时的问题就是等式约束下的求极值问题,用拉格朗日乘数法求解即可。
这两部分对应到样本上,又是什么?
- 当可行解$W$落在 $g_{i}(W)>0$内时,此时$i$这个样本点是“马路”之外的点;
- 当可行解$W$落在 $g_{i}(W)=0$内时,此时$i$这个样本点正好落在马路边上,也就是我们的支持向量!
我们再进一步思考下:
- 当可行解$W$落在 $g_{i}(W)>0$内时,此时约束不起作用(即求无条件极值),也就是拉格朗日乘数 $\lambda_{i}=0$;
- 当可行解$W$落在边界上时, $\lambda_{i}\neq 0 ,g_{i}(W)=0$。 不论是以上哪种情况, $\lambda_{i} g_{i}(W)=0$ 均成立。
搞懂了上面说的,接下来构造拉格朗日函数,$n$个不等式约束都要加拉格朗日函数 $\lambda_{i} \geqslant 0$ ,有拉格朗日乘数向量 $\lambda =(\lambda_{1},\cdots\lambda_{n})^{T}$ :
\[L(W,b,\lambda ) = f(W)-\sum_{1}^{n} \lambda_{i} g_{i}(W) =\frac{||W||^{2}}{2} - \sum_{1}^{n} \lambda_{i}y_{i}(WX_{i}+b) +\sum_{1}^{n} \lambda_{i} \tag{1}\]要求极值,先对参数求偏导:
\[\frac{\partial L}{\partial W}=W-\sum_{1}^{n} \lambda_{i}y_{i}X_{i}=0 \tag{2}\] \[\frac{\partial L}{\partial b}=\sum_{1}^{n} \lambda_{i}y_{i}=0 \tag{3}\]此时又要引入一个概念——对偶问题。关于对偶问题可以参见这篇文章,这里再不赘述。简而言之就是原先的问题是先求$L$对$\lambda$的最大值再求对$W$、$b$的最小值,变成先求$L$对$W$、$b$的最小值再求$\lambda$的最大值。
将(2)式 $W=\sum_{1}^{n} \lambda_{i}y_{i}X_{i}$ 代入(1)式,得:
\[\begin{aligned} L &= \frac{1}{2}(\sum_{1}^{n} \lambda_{i}y_{i}X_{i})(\sum_{1}^{n} \lambda_{i}y_{i}X_{i}) - \sum_{1}^{n} \lambda_{i}y_{i} ((\sum_{1}^{n} \lambda_{i}y_{i}X_{i})X_{i}+b)+\sum_{1}^{n} \lambda_{i} \\ &= \sum_{1}^{n} \lambda_{i} - \frac{1}{2}(\sum_{i=1}^{n} \sum_{j=1}^{n} \lambda_{i} \lambda_{j}y_{i}y_{j}X_{i}^{T}X_{j}) \end{aligned} \tag{4}\]此时目标函数中$W$、$b$就都被消去了,约束最优化问题就转变成: 目标函数:
\[\min L(\lambda ) = \min \left(\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} \lambda_{i} \lambda_{j}y_{i}y_{j}X_{i}^{T}X_{j}-\sum_{1}^{n} \lambda_{i} \right) \tag{5}\]约束条件: \(\sum_{1}^{n} \lambda_{i}y_{i}=0 , \lambda_{i} \geqslant 0 \tag{6}\)
\[\lambda_{i}\left( y_{i}(WX_{i}+b)-1\right) = 0, i=1,2\cdots n \tag{7}\](6)式来自上面的(3)式,(7)式是由 $\lambda_{i} g_{i}(W)=0$ 而来。如果能解出上面这个问题的最优解,我们就可以根据这个 $\lambda$ 求解出我们需要的$W$和$b$。
5. 线性可分问题小结
最大边界超平面是由支持向量决定的,支持向量是边界上的样本点:
- 假设有$m$个支持向量,则 $W=\sum_{1}^{m} \lambda_{i}y_{i}X_{i}$;
- 从$m$个支持向量中任选一个,可以求 $b=y_{i}-WX_{i}$;
- 决策函数 $h(x)=\text{sgn}(W^{T}X+b)=\text{sgn}\left[\sum_{1}^{m} (\lambda_{i}y_{i}X_{i}^{T})X+b\right]$;
- 对新样本 $X_\ast$的预测: $\text{sgn}(W^{T}X_\ast+b),W^{T}X_\ast+b$为正则 $y_\ast=1$,为负则 $y_\ast=-1$,为$0$则拒绝判断。
至此我们讲完了线性分类支持向量机的逻辑思想和求解过程,但这些只是SVM的基础知识,真正的核心其实还没有讲到。要知道,SVM的优势在于解决小样本、非线性和高维的回归和二分类问题(Support vector machine, SVM, 1992, Boser, Guyon and Vapnik)。
- 小样本,是指与问题的复杂度相比,SVM要求的样本数相对较少;
- 非线性,是指SVM擅长应付样本数据线性不可分的情况,主要通过核函数和松弛变量来实现,这才是SVM的精髓,而本文是入门笔记,暂不涉及;
- 高维,是指样本维数很高,因为SVM 产生的分类器很简洁,用到的样本信息很少,仅仅用到支持向量。由于分类器仅由支持向量决定,SVM还能够有效避免过拟合。
参考链接
SVM 原理详解,通俗易懂_DP323的博客-CSDN博客_svm